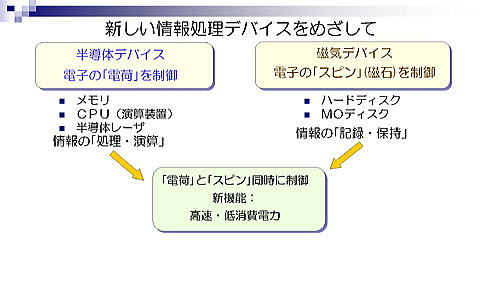
高橋研究室では固体中の電子の「スピン」に着目した研究を行っています

磁気緩和定数の測定

強磁性体金属では磁気緩和の速さを決めるパラメータである磁気緩和定数(Gilbert damping constant) alphaが重要になります。 （下記項目「半導体−磁性金属接合の作製」も参照してください）　 　　例えば半導体メモリーの置き換えを目指して近年開発が進んでいるSpin Random Access Memory (SpinRAM) ではメモリーの状態を制御するために電流を注入します。消費電力と発熱を抑えるためには小さい電流で制御したいのですが、必要な電流の大きさがalphaに比例しているため、alphaが小さい磁性材料を使うことが望ましいということになります。素子を作る上では他の磁気特性、例えば飽和磁化とか磁気異方性定数も重要で、これらとalphaの関連も考慮する必要があります。alphaの大きさを決めている要因が飽和磁化や磁気異方性にも影響を与えるのであれば、alphaの値を小さくしようとすると他の磁気特性も変化してしまい、素子の動作特性を悪化させる恐れがあります。 　　このように物質のalphaの値がどのような原因で決まっているか、そしてそれと他の磁気特性はどのように関連しているのかを知ることは素子の材料を探索する上で重要な指針を与えます。理論研究によるとalphaは　（1）結晶構造、（2）スピン−軌道相互作用(SOI)、（3）電子散乱頻度、（4）フェルミ面付近の電子密度、に依存すると考えられています。そこで比較的小さいalphaを持つことが知られている典型的な3d遷移金属磁性体である鉄（Fe）をベースとして、これに同じ3d元素であるコバルト(Co)やニッケル(Ni)などを微量添加した薄膜試料を作製して、それらのalphaおよび他の磁気特性を測定します。CoあるいはNiの添加量は小さい（10 at. %以下）ので結晶構造はFeと同じです。しかしスピン−軌道相互作用はFeから変化していきます。また一様なFeの中に少数含まれた異種原子であるCo, Niは電子に対する散乱体として働くので電子散乱頻度が上昇していきます。さらにCo, NiはFeよりも電子数が多いので、これらを添加するとフェルミ面が高エネルギー側にシフトします。 　　微量に添加した不純物原子はこれらの効果を通してalphaおよび磁気特性に影響を与えると考えられます。添加原子の種類、濃度を変化させてその効果を測定することによりalphaの起源について重要な情報をもたらしてくれると期待しています。現在CoおよびNiを添加した薄膜で測定を行っています。

この研究の一部は科学研究費補助金（基盤研究（C)：課題番号23560384）の支援を受けて行われました。 論文：　Journal of Magnetic Society of Japan, Vol. 37, No. 3-2, p. 166 (2013)

半導体‐磁性金属接合の作製
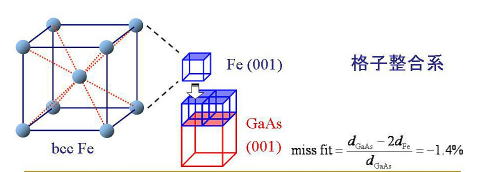素子が機能するためには強磁性体金属と半導体の間でスピン偏極を保ったままで電子をやり取りする必要があります。強磁性金属と半導体接合の典型的な例として鉄(Fe)-ガリウムヒ素(GaAs)接合の研究が広く行われています。この組み合わせではFeの格子定数の2倍がGaAsの格子定数にほぼ等しいので、上の図に示すように格子整合した結晶成長が可能になります。この系ではこれまでに分子線エピタキシー法(MBE)による結晶成長が行われてきました。金属の成膜法として広く使われているもうひとつの結晶成長法としてスパッター法があります。MBE法に比べて成膜速度が速く、量産に適した方法と考えられています。 　RFマグネトロンスパッター法によりGaAs(001)面上にFe(001)面薄膜を成長し、X線回折により、その構造を評価しました。下に示した図がX線回折法の一つである極点図(Pole Figure)測定で、2theta = 44.4度に設定したときの測定結果です。極角45度付近で、GaAs基板{011}面からの強い回折に隣接してFe{022}面からの回折が4回対称を示して観測されています。これはGaAs(001)面上にFe(001)面がcube-on-cubeの配向でエピタキシャル成長していることを示しています。
次に試料振動型磁力計(VSM)と強磁性共鳴(FMR)測定装置を用いて、作製されたFe薄膜の磁気特性を評価しました。左下に示した図が膜厚12 nmの試料に対するVSM測定結果です。1.7 kemu/ccを超える大きさの飽和磁化が測定され、また面内で印加磁場方向を変えて測定したところ、<100>方向が磁化容易軸、<110>方向が困難軸であることが示されています。飽和磁化の大きさ、ループの形ともに、良く知られているFe単結晶のデータによく一致しており、高品質のFe薄膜であると考えられます。 　右下に示した図はFMRによる測定結果で、面内の印加磁場角度と、共鳴磁場（上のグラフ(a)）および共鳴線幅（下のグラフ(b)）の関係を表しています。共鳴磁場(a)の大きさは面内磁気異方性を反映しており、膜厚6 nmと12 nmの試料ともに<100>方向が磁化容易軸、<110>方向が困難軸であることを示しています。これはVSMの測定結果とも一致します。 　FMR線幅は磁性材料中の磁気緩和、つまり外部からの力により向きの変化した電子スピンが定常状態へ戻るまでの時間を反映しています。狭い共鳴線幅は磁気緩和率が小さいことを示しています。磁気緩和現象はLandau-Lifshitz-Gilbert方程式により理論的に記述され、この中に現れる無次元のパラメータであるGilbert damping constant, alphaが磁気緩和の速さを決めます。共鳴線幅から求めたalphaの値がグラフの右側軸に示されています。この研究で作製したFe薄膜では、共鳴線幅は小さい値を示しており、特に膜厚12 nmの試料ではalphaに換算して0.003―0.004というきわめて小さい磁気緩和を示すとともに、印加磁場方向には依存しないという特徴を示しています。 　電子の持つ角運動量(スピン）を直接使った磁化制御法として注目されている電流注入磁化反転において、試料の磁化を反転するのに必要な電流はalphaの値に比例すると考えられています。この技術をデバイスに使った場合に、その消費電力を低減する、あるいは発熱を抑制するにはalphaが小さい材料を使う必要があります。磁気デバイスの製造に通常使われているスパッター法で作製したFe/GaAs薄膜においても小さいalphaを示すということは、電流注入磁化反転の実用化を考えるとき重要な実験事実であると考えています。
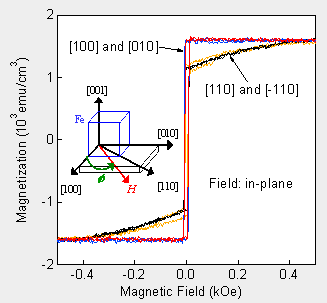膜厚12 nmのFe薄膜に対するVSM測定結果 磁場は面内で向きを変えて測定した。		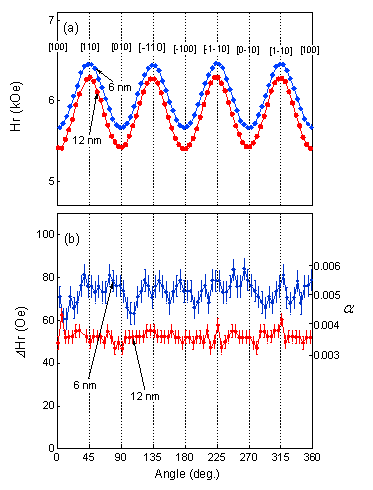FMRにより測定した共鳴磁場(a)と共鳴線幅(b)
この研究の一部は科学研究費補助金（基盤研究（C)：課題番号20560315, 23560384）の支援を受けて行われました。 論文：　IEEE Transactions on Magnetics, Vol. 47, No. 12, p. 4682 (2011) 国際会議：　PASPS-VI, ISAMMA 2010

半導体‐磁性金属接合におけるスピンダイナミクス

多くの素子では強磁性体（金属）の電極から半導体の中へ（あるいはその逆向きに）スピン偏極電子を注入することによりいろいろな機能を発揮します。電子スピンの向きがそろった強磁性体の中に、外から逆向きのスピンを持った電子を注入すると、磁性体内のスピンがいっせいに反転する現象(スピン注入磁化反転）が見出され、スピン偏極電流により磁化を制御する方法として注目されています。 　この現象を磁気記録の高速化と微細化に応用することができないかと考えて研究を行っています。磁化反転速度と反転電流の大きさは磁気緩和係数(Gilbert damping constant)により決定されるので、半導体上の強磁性金属薄膜（たとえばGaAs上のFe膜）でこの係数の値がどのようになるかを強磁性共鳴法により測定しています。また薄膜の磁気特性は磁気光学カー効果などを使って測定しています。

この研究の一部は科学研究費補助金（基盤研究（C)：課題番号20560315）の支援を受けて行われました。 論文：J. of Appl. Phys., 104 023714 (2008)

スピン偏極系における移動度及び拡散係数への電子‐電子相互作用の効果

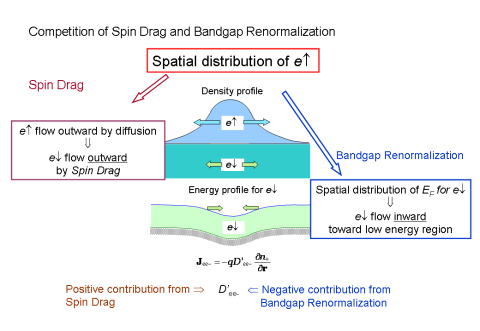
電気抵抗や高周波特性など素子の動作特性は素子中の電子輸送係数（移動度と拡散係数）により決まります。そして、この輸送係数は材料中での電子の散乱により支配されています。現在使われている半導体素子では低温（液体窒素温度以下、< 77 K)では電子とイオン化不純物との散乱が、そして室温程度の温度領域では電子と光学フォノンとの散乱が輸送係数を決める要因になっています。電子同士の散乱も頻繁に起きていますが、これは弾性散乱で運動量が保存するために電子全体の輸送には影響を与えません。 ところがスピンに依存した素子ではスピン上向きの電子とスピン下向きの電子を別々に取り扱うことになります。このためスピン上向き電子と下向き電子との散乱が起きるとスピン上向き電子系から下向き電子系へ(あるいはその逆向きに）運動量が移行して、それぞれの系の電子輸送が影響を受けます。つまりこれまでの素子では寄与のなかった電子‐電子散乱が、これらの素子では電子輸送係数に影響を及ぼすことになります。上の図に示したように、スピン下向き電子の濃度は空間的に一様で、スピン上向き電子の濃度が釣鐘型の分布を持つ場合を考えます。(電場を印加しない場合でも）スピン上向き電子は拡散により中央から周辺向かって流れます。この拡散流に引きずられてスピン下向き電子も周辺に向かって流れることになります。(この現象はSpin Dragと呼ばれます。） これに加えて、伝導帯に多数の電子が存在する場合には、単一の電子しか存在しない場合に比べて、電子のエネルギーが変化します。（Bandgap Renormalizationと呼ばれます）　これは電子間のクーロン相互作用によるMany-electron effectsのひとつです。この効果も電子輸送に影響します。上の図に示したようにスピン上向き電子が釣鐘型の分布を持つ場合に、一様な分布を持つスピン下向き電子のエネルギーバンドが変化して、中心部のエネルギーが低下します。電子はエネルギーが小さくなる向きに流れますからこの場合にはスピン下向き電子が中心に向かって流れることになります。 このように、素子中の電子輸送では電子‐電子相互作用によるSpin DragとBandgap Renormalizationを考慮する必要がでてきます。私たちの研究ではGaAsからなるスピン偏極2次元電子系における電子の輸送係数を計算により求めました。これによると、 （１）低温域（< 70 K)：輸送係数は電子‐電子相互作用の影響を強く受ける。スピン偏極系の場合多数スピン系の移動度は少数スピン系のそれよりも大きくなるが、Spin　Dragはこの差を小さくする効果がある。 （２）室温付近：移動度は電子間散乱の影響を受けなくなる。この温度域ではもともと電子‐光学フォノン散乱が支配的だが、これはスピン上向きと下向き電子に同じ移動度を与える。このため電子間散乱の効果を含めても移動度は変わらない。これに対して拡散係数は室温域でも電子‐電子相互作用の寄与が残る。これは、室温域で使用する素子でも、電子‐電子相互作用を含めた輸送係数を使ってデバイス設計を行う必要があることを示している。

この研究の一部は科学研究費補助金（基盤研究（C)：課題番号16560002）の支援を受けて行われました。 論文： Jap.J. of Appl. Phys. Pt.1, 46 2585 (2007) J. of Appl. Phys., 101 093707 (2007) phys. stat. solid. (c), 5 314 (2007)

化合物系半導体中をスピン緩和現象

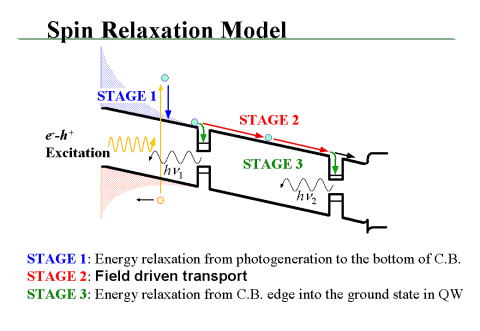
通常の半導体素子では電子の電荷を使って機能しています。電荷は保存します。途中で消えてしまうことはありません。しかし，スピンを活用した素子では、その機能をになうスピンは「緩和」してしまい，消えてしまうことがあります。伝導中のスピン緩和は素子の機能を考える上で重要な要素になります。この研究では半導体(GaAs)中に円偏光により光励起された電子のスピンが電場によりドリフトする間に，どこで，どれだけ速やかに緩和していくのかを実験で検討しました。 　測定は分子線エピタキシーによって作製された厚さ4ミクロンのGaAs試料に対して行いました。バンドギャップに相当する波長の円偏光の短パルス光を入射して表面付近にスピン偏極電子を生成します。この電子は印加した電場により試料の中にドリフトにより流れます。(同時に生成される正孔はバイアス電場により表面電極側に流れ去ります。）試料の表面から2ミクロンと4ミクロンの部分に厚さが異なるInGaAsの量子井戸構造が形成されており、表面からドリフトしてきた電子の一部はまず1番目の井戸に落ち込み発光再結合をおこします。この発光の円偏光度を測定することによりこの部分での電子のスピン偏極度を測定することができます。更に電子は試料奥に2ミクロンだけドリフトして行って、2番目の井戸に落ち込んで発光再結合します。この部分の電子スピン偏極度はやはり発光の円偏光度を測定することにより知ることができます。1番目の井戸の位置でのスピン偏極度と2番目の井戸付近でのスピン偏極度を比べることにより、ドリフト中にどれだけスピン緩和が起きたかを知ることができます。励起波長、印加電場を変えて測定を行うことにより、電子輸送のどの過程でスピン緩和が起きているのかを調べました。 　これらの実験の結果、電場中をドリフトする電子のスピン緩和は印加電場に強く依存することがわかりました。電場が強くなるとスピン緩和はより高速になります。また光励起直後に電子がバンド端までエネルギー緩和する間のスピン緩和は小さいこと、これに比べバンド端から更に量子井戸に落ち込む際のスピン緩和がかなり大きいことが判明しました。いくつかの提案されている素子では量子井戸中にスピン偏極電子を注入する必要があるので、この過程でのスピン緩和は素子の機能に影響を及ぼす可能性があります。

この研究の一部は科学研究費補助金（基盤研究（C)：課題番号16560002　および　14550001）の支援を受けて行われました。 論文：Jap. J. of Appl. Phys. 43 L230 (2004) 国際会議：CLEO/Europe-EQEC2003, SSDM2003, PASPSIII (2004)

半導体低次元構造中のスピン偏極電子輸送現象

相互作用しているスピン偏極した縮退フェルミ粒子系では，スピン拡散の振る舞いが，自由粒子系のそれとは大きく異なることが知られており，LeggettとRiceは，スピンエコー法によって測定される横スピン拡散係数が最初のrfパルスによりスピンの傾けられる角度に依存することを理論的に示しました。（Leggett-Rice効果）これは相互作用しているフェルミ流体中におけるスピンカレントの輸送方程式の中に，他のスピンが作る分子場によってスピンカレントが歳差運動を行う項(spin-rotation 項)が含まれるためです。またスピン偏極した粒子系にはスピン波が現れることも示されています。これらの効果は，”Spin-rotation効果”と総称され，液体4He中の希釈3He，気体・液体3He、そしてバルクの金属を対象にして多くの実験が進められてきました。 　この研究では半導体微細構造中に作られる、高品質の２次元スピン偏極電子系を対象として、これに量子力学的輸送方程式を適用し，そのスピン輸送の振る舞いを理論的に解析しました。これにより低温（電子分布が縮退した領域）における縦および横スピン拡散係数を数値的に求めました。縦スピン拡散係数は温度が下がるに従い単調に増大しますが、横スピン拡散係数は低温でその増大が飽和することが示され、その飽和拡散係数の大きさは系のスピン偏極度に依存しています。これは後者が通常のフェルミ流体の輸送係数の温度変化とは異なる振る舞いをすることを示しています。またスピン波などのスピン集団運動発生の目安となるSpin-rotation parameterは低温で増大し、半導体中の2次元電子ガスにおいてもLeggett-Rice効果が発生し得ることを示しています。

この研究の一部は科学研究費補助金（基盤研究（C)：課題番号11640307）および奨励研究（A)(萌芽的研究）の支援を受けて行われました。 論文：Phys. Rev. B60 4856 (1999) 国際会議：PASPS2000 (Physica E10 22 (2001))